Suppose you are presented with two doors. Behind each door is a cash prize. You are told that one of the prizes is exactly twice as much as the other. You can choose either door and get what's behind it. You choose a door. Now, before finding out what's behind it, you are given the option to switch doors and take the other prize instead. Should you switch? Common sense dictates that it doesn't matter; you've been given no additional information.
But look at it mathematically. Let N represent the prize (in dollars) behind your door. The prize behind the other door is either ½N or 2N (with equal probability). That means that the expected value of the amount behind the other door is 1.25×N (calculated as ½×(½N) + ½×(2N)). So, by switching you increase your expected prize from N to 1.25×N.
But that can't be right. And to emphasize, you can do the switch and then be faced with the same conundrum. Your new prize is X, but by switching back you have an expected prize of 1.25×X. And you can keep going back and forth, forever increasing your expected prize.
So where's the flaw? I note, by the way, that showing that there is a flaw (as done in the last paragraph) is not the same as finding the flaw. What assertion is it that's wrong?
While you're thinking, I'll separate the question from the answer with this charming video.
The mistake is in the statement, "That means that the expected value of the amount behind the other door is 1.25×N (calculated as ½×(½N) + ½×(2N))." That statement implicitly assumes that, regardless of whatever value is behind the door you chose, the other door is equally likely to have twice that amount and and to have half that amount. But that assumption is faulty; there is no probability function (or probability distribution function if you want to work in the continuous world) that will give you that property.*
In the remaining paragraphs, I will use the convention that you initially choose door A. I will use VA to indicate the value behind door A. B represents the other door and VB represents the value behind door B
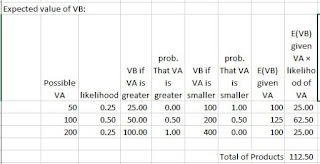
To calculate the expected value if you don't switch, you have to multiply all the possible values of VA by their respective likelihoods and then add up the products. Of course, to calculate your expected winnings if you switch, you do the same thing for B and get the same result. But if you want to avoid explicitly assuming that they're the same (which kind of renders the proof that they're the same moot), you have to look at all the values of VA, then get the expected values of VB conditional on VA, and multiply them by the likelihoods of the respective possible VAs.
To take a simple example, assume that there are two possible pairs of values for the two doors: (50, 100) and (100, 200). The possible values of VA are 50, 100 and 200. These have likelihoods ¼, ½ and ¼. So the expected value of VA is 112.5, calculated as follows:
Calculating the expected value of VB involves more calculations, but none of them is particularly difficult. You need each value of VA and its likelihood. Then you need to calculate the expected value of VB given the value of VA. To do that, you have to look at the values of VB if VA is the greater of the two and if VA is the lesser of the two, and the likelihoods of all those. Calculating the expected value of VB yields 112.5, which is the same as the expected value of VA.
QED.
*Put more exactly, for all values X, the probability that the two prizes are ½X and X is equal to the probability that the two prizes are X and 2X. That's mathematically impossible unless you're taking the trivial case where X is equal to zero with probability 1.

No comments:
Post a Comment